Frequently Asked Questions

Cast in varying forms, this has been a very active question over the past year. Addressing it was a primary reason for writing Probable Outcomes. The book not only answers the question, but also builds the proof, quantifies the range of outcomes for this secular bear, and describes the implications for a variety of investors.

But if you don’t have time for the book or if you just want the answer and not the proof, here’s the summary. No, a secular bull has not started and is not near. Actually, the current level of P/E (relatively high–see “The P/E Report” on this website) is closer to secular bear starting levels than it is to the end or even the midpoint.

The level and trend of P/E drives the long-term secular cycles, but technically it is only “involved with” short-term cyclical cycles.

To qualify as a “secular” cycle, P/E must grind higher or lower over an extended period, specifically due to an adverse trend in the inflation rate. The result is an extended era–or secular period–when P/E has a significant effect on stock prices.

When P/E becomes misaligned with fundamental principles (e.g., in financial crises, sudden crashes, or euphoric bubbles), the move into misalignment is short-term or cyclical and the restoration to general alignment is also cyclical.  Cyclical moves occur fairly quickly once emotional forces dissipate. The recent 2008 decline and 2009/2010 recovery are classic examples of cyclical bear and cyclical bull cycles.

Here are 12 rules of secular stock market cycles:

1. Secular cycles are driven by the inflation rate (deflation, price stability, and higher inflation).
2. Secular bulls occur when P/E starts low and ends high over an extended period.
3. Secular bears occur when P/E starts high and ends low over an extended period.
4. Cyclical bulls and bears are interim periods of directional swings within secular periods.
5. Cyclical cycles are driven by market psychology, illiquidity, or other generally temporary condition(s).
6. Time is irrelevant to the length of secular stock market cycles.
7. Secular bulls require a doubling or tripling of P/E.
8. Secular bears occur as P/E stalls and falls by one-third to two-thirds or more.
9. When real economic growth is near 3%, there is a natural floor for P/E between 5 and 10, a natural ceiling around the mid-20s, and a typical average in the mid-teens.
10. If economic growth shifts upward or downward for the foreseeable future, the natural range of P/E likewise moves upward or downward.
11. Inflation drives P/Es relative position within the range; economic growth drives the level of the range.
12. The stock market is not consistently predictable over months, quarters, or periods of a few years. The stock market is, however, quite predictable over periods approaching a decade or longer, based upon starting P/E.

For example, assume the market crashes in half today, pulling P/E toward 10 but without a change in the outlook for inflation or deflation. Then market psychology or illiquidity remains mired in crisis for a week or a year or longer. The downdraft is a cyclical bear.  Once conditions calm, much like a tightly wound spring waiting for freedom, the market will recover to a higher level based upon price stability. The upswing is a cyclical bull. The key point is that the upswing restores the market to a high P/E.  Once that happens, even though P/E spent time near 10, it is no longer positioned for a secular bull. A secular bull cannot start from high P/Es–a secular bull requires a doubling or tripling of P/E over time.

To further illustrate, a secular bull occurs following a case of the financial flu–after the economy has slipped progressively into deflation or inflation from a condition of price stability.  The progressive worsening of conditions under deflation and inflation will have pushed P/E toward 10–or certainly well below average.  Then, as a result of improving conditions (which historically have required years and often decades), P/E progressively rises. As it doubles or triples over five, ten, or twenty years, the multiplier effect compounds earnings growth and delivers long runs of positive years and above-average returns.

Many people mistakenly assume (or hope) that P/E touching base below average–even if it quickly recovers–enables a secular bull era. It’s not so simple. The missing prerequisite is that P/E must be positioned to double or triple in order to produce a secular bull.

The Crestmont Matrix shows that long-term average returns represent the combination of below-average and above-average decades.  Further, the periods are primarily driven by the starting P/E.  As a result, the Crestmont Matrix helps investors know to invest differently today than they invested in the 1980s and ‘90s.  Investors must take action to plan for lower returns from traditional buy-and-hold stock and bond market investments.  Investors can take a more diversified and active-management approach of “rowing” across extensive periods of volatility rather than passively “sailing” with the momentum of a secular bull market.  Early recognition and planning enables investors to adjust expectations and strategy.

The Crestmont Stock Market Matrix presents the returns from the stock market, using the S&P 500 Index, for all combinations of periods from 1900 to present.  Each colored square and number in the field of the graph reflects a period driven by a starting year from the left axis and an ending year from the top axis.  The number in the square is the compounded annual return across the period; the color of the square indicates the magnitude of return.

First, the Crestmont Stock Market Matrix should be viewed from a distance, much like a Magic Eye image which reveals its picture as you stare at the whole at once.  The Crestmont Matrix reveals a heat map of returns that tells the story of calm blue average returns over the long-term–even as the long-term encompasses dramatic periods of a decade or longer along the horizon that reflect significant surges of well above-average returns punctuated by extended periods of stall resulting in well below-average returns.

Second, stock market returns are not random; they occur across extended periods driven by the trend in the price/earnings ratio (P/E).  The numbers within the graph are presented in black and white.  Black numbers reflect an increase in P/E over the period, while white numbers correspond to a decreasing P/E.  Note that green periods generally reflect black numbers and red periods reflect white numbers.

Third, the Crestmont Matrix delivers complementary views of history to emphasize that the current period is not unique.  Although the current era includes seemingly dramatic events and revolutionary technology, a walk down the right margin reveals that similar leaps in technology have occurred during almost every decade in the past century.  Likewise, a walk across the economic measures on the bottom of the chart similarly reveals a common long-term trend that generally continues today.  Neither the major events nor economic measures of today suggest that the current period and future decades will be different from the past.  Stock market history repeats itself, with slightly different rhymes.  The lessons of history are good indications for what is needed to be successful in the future.

Finally, the version of the Crestmont Matrix that presents real returns, excluding the effects of inflation, better reflects the purchasing power of returns from investments.  Periods with high inflation overstate the value of returns.  Conversely, breaking even in the stock market during a period of deflation can provide greater purchasing power than positive returns that don’t keep up with inflation.

One of Crestmont’s most recognized presentations is the Stock Market Matrix, the multicolored mosaic of investment returns over the past century. The Stock Market Matrix was one of Crestmont’s first research initiatives. In the summer of 2001, the objective was to determine whether the stock market had completed its retreat from recent highs and would soon return to new territory, or whether the pullback was far from complete. In a discussion with an experienced investor, debate raged about long-term returns in the stock market and whether the trend had made its way back to the level that would allow average returns in the future. The crux of the discussion focused on the returns that are typically presented–the long-term return series of seventy-five years or more that is often used by investors and investment advisors.

Some of the most popular presentations of long-term stock market returns arbitrarily start in the 1920s and determine the returns through the present. The first question was whether that starting date is reasonable or whether it distorts the analysis.  If the starting level in the stock market is the high in 1929, the returns are quite different than if the starting level is the low that occurred after the crash in 1929. An analysis of returns that is dependent on a single starting point may produce invalid information.

After many long hours, a detailed presentation was developed. Rather than start at one date in the distant past, multiple starting points at the beginning of every decade were chosen.  The result was eleven sets of analyses laid out for consideration. Almost conclusively, they reflected that the market remained overvalued to various degrees. The astute investor, however, identified another vulnerability when he asked, “But isn’t the analysis still subject to single-point risk? What if the start of every decade distorts the results for some reason?”

In response to the challenge, the Crestmont Stock Market Matrix was developed as a method to present every annual return scenario since 1900. The Crestmont Matrix provides every starting year and every ending year, and then calculates the annualized return for the periods. In addition, the Crestmont Matrix uses modes of coloration and ancillary information to enhance its effectiveness as a communication tool. Returns are denoted in shades of red, blue, and green to reflect the level of returns. Further, information about economic growth, inflation, and historical events over the past century are included to add depth to the chart’s messages. Today, around the world, hundreds of thousands of copies of the Stock Market Matrix have been downloaded from CrestmontResearch.com.

The area in the Y that is most out of place is the zone on low inflation and low P/E. For illustration, let’s focus on the dots for years with the inflation rate between -1% and 3% (2 pts either side of 2% inflation) and P/E below 15.

There are 16 points that represent seven periods (a number of the dots reflect two or more years in succession). These points occur for various reasons. Most often, the periods are fast transition points from deflation to higher inflation or periods where deflation and inflation were churning back and forth (e.g., 1913-1915, 1923-1926). The inflation rate was much more erratic before the 1950s.

Of the seven periods, five occurred before 1950. One of the seven periods occurred in the 1950s (1950-1954, excluding 1951). In the years before that period, the inflation rate was fairly high and erratic…in 1951, the inflation rate spiked to 8%. Apparently it took quite a few years across the early 1950s to convince the market that inflation was coming under control…after 1954, P/E surged and ultimately ended that secular bull at 23.

In the past 60 years, since 1954, there was only one year in the group of seven: 1986. During 1986, the inflation rate experienced a sudden and significant drop in the inflation rate…the years before and after that year averaged 4%-5%. Therefore, 1986 was an outlier in the trend of relatively high inflation—it was not an indication of a decline toward price stability. A Y Curve chart for the years 1955-2013 shows a tighter relationship to the upper fork of the Y Curve and excludes the deflation periods (occurring prior to 1955) associated with the lower fork of the Y.

First, let’s establish that the relationship between P/E and the inflation rate is based upon financial principles. It is not a relationship of coincidence. Stocks are financial assets whose value is determined by their future cash flows in the form of dividends and retained earnings. The current value of a stock is based upon the market’s expectation for future earnings (in the long-term) and a discounting rate of return. The future cash flows are subjectively assessed based upon likely growth rate and business prospects. The discounting rate is based upon market rates for financial assets and individual company risk (consistency of earnings, likelihood of future success, etc.). Market rates are driven by the inflation rate, as investors price financial assets to compensate for inflation. Whereas an individual stock has part of its value determined by individual characteristics, the overall market aggregates (and thus mitigates) the individual company premiums or discounts. Therefore, stock market valuation (as measured by P/E and other measures) is largely driven by the inflation rate and the expected future growth rate for earnings (which for the overall market is driven by the rate of economic growth). In academic terms, the value of the stock market is based upon the present value of future cash flows using a discount rate that varies primarily with changes in the expected inflation rate.

As an aside, prior to 2000, economic growth was fairly consistent over extended periods of time; thus the growth rate had little impact on long-term valuations. The slower economic growth since 2000, as well as other demographic changes expected for the future, has driven many economists and analysts to expect future economic growth to be slower than historical economic growth. If so, growth could become another factor impacting P/E.

Therefore, we can conclude that the level of P/E is driven by the level and trend of the inflation rate–keeping in mind that short-term volatility and general subjectivity cause P/E to fluctuate significantly in the short-run. With that in mind, let’s explore past secular cycles using the Secular Cycles Profile (especially since the level of detail in the Dashboard makes it hard to line up the various relationships for the purpose of assessing past cycles; the Dashboard is intended to be used to assess the consistency of key measures currently).

The first secular stock market cycle of the 1900s started in 1901. It has thus far been the longest secular bear market and it lasted 20 years. Over the first 5 years of that secular bear, P/E started at 23 and averaged near 20; the inflation rate was choppy, yet averaged near 1%. During the middle 10 years, the inflation rate began to gyrate more dramatically from year to year between significant inflation and deflation (a lack of price stability); as a result, P/E declined to average near 14. In the last 5 years of that secular bear, the inflation rate surged into the teens, thereby driving P/E to 5.

The subsequent secular bull market started in 1921 with a pair of years in deflation, yet the market apparently anticipated that the inflation rate would be soon headed toward price stability. Both 1921 and 1922 delivered gains and started P/E on its track upward. By 1928, the inflation rate was near zero, and P/E had returned to levels in the 20s. The peak in P/E occurred in 1929, the first year of the subsequent secular bear. Note that when it’s unclear which of two years is the end of one cycle and start of another, the rule is that secular bulls never start with a down year and secular bears never start with an up year.

The 1929 secular bear lasted four years as P/E declined to 8 while the economy fell into significant deflation. By 1933, deflation began to give way to low inflation, and P/E responded by rising to 19. The cycle shifted again in 1937 as the inflation rate became erratic and ultimately reached 11% six years later, thereby driving P/E to a secular cycle low of 9. The shuffle-step series of three secular stock market cycles over 13 years is rarely delineated by most secular cycle analysts. The entire period is often aggregated for convenience to create the appearance of a similar length to other secular periods. But the aggregation eliminates the key insight about secular stock market cycles. The dramatic shifts and trends in the inflation rate drove P/E between highs and lows three times over that thirteen years. This period emphases the link between the inflation rate and P/E.

The longest secular bull started in 1942: it would ultimately run 24 years. In 1942, inflation crested at 11%, and P/E troughed at 9. For most of the first half of that secular bull, the inflation rate gyrated across high and low levels with P/E staying at or just above 10. Once the inflation rate began to stabilize in the late 1950s, P/E started climbing and ultimately reached 23 by 1964. In 1966, the inflation rate began to show signs of a gradual increase, and P/E started declining again; the most recent secular bear had begun. It would last 16 years as the inflation rate marched over 10% and P/E declined to 7.

Then came the most significant secular bull of all time. The inflation rate descended slowly until it ultimately reached 2%. Responding to the moderation of the inflation rate, P/E rose from 7 to normal secular bull highs in the mid-20s, then doubled again to pierce an extreme high over 40. As it become clear that future economic growth rate would not be elevating as a result of new technologies, the market bubble popped. The first part of the current secular bear, which started in 2000, was a readjustment of ultra-high P/E to normally-high P/E. P/E is expected to be high when the inflation rate is low. Current conditions reflect a normal relationship of low inflation and high P/E. The market is relatively close to fairly-valued.

Yet, fairly-valued does not indicate that average returns are ahead. Fairly-valued means that the market is priced appropriately, given a low inflation rate. Higher valuations produce below average returns due to lower dividend yields and the potential (likelihood at some point) of lower future P/E. A declining P/E offsets some or all of earnings growth and leads to significantly below-average returns. Even without a decline in P/E, returns from points with a high P/E are below average.

So have there been exceptions? Not in principle. Although a strict analysis of reported numbers for the inflation rate and P/E from year to year does not confirm a tight relationship between the two variables, an analysis that permits a reasonable level of variability in magnitude and time clearly demonstrates the cause-and-effect relationship that is consistent with financial principles. High inflation drives high discount rates and lower stock market valuations. A return to low inflation leads to lower discount rates and higher stock market valuations. Deflation drives future cash flows lower in nominal terms, leading to lower stock market valuations. A reasonable level of variability is needed to incorporate expectations and actions that may not be evident in raw historical numbers.

To explain why higher inflation drives down P/E, let’s first think about the phenomenon of inflation itself. We talk about inflation whenever prices go up, but not all price increases are inflation. When the price of one thing or a few things goes up, that’s just a price increase. When the aggregate price of everything that you buy increases, that constitutes inflation.  Inflation occurs when the federal government prints more money than the value of goods in the economy. The result is that the prices of things adjust upward to reflect the loss of money value.

That’s where interest rates come into the picture. Interest rates help to offset the loss of value due to excess money creation. That’s also why interest rates go up as inflation rises and fall as inflation declines. This is why bond prices and yields rise and fall as the expected inflation rate changes.

To illustrate, consider that bonds are financial securities that pay interest over time. A $100 bond with the interest rate of 5% pays $5 per year throughout its term. When market interest rates, as driven by inflation, are 5% then the bond is worth $100. But what happens when inflation rises and market interest rates go to 10%?  Well the bond is not worth as much. Actually, the price of the bond declines so that the $5 interest payment and the $100 maturity value will yield 10% over the life of the bond. The key point is that rising inflation drives bond prices lower. Conversely, falling inflation makes those bond payments worth more since new bonds will pay lower interest payments. The result between bonds prices and inflation is a fundamental relationship driven by principles of finance.

Now let’s consider the stock market. Stocks are also financial assets. They often pay dividends from earnings quarterly or retain the earnings to build more value in the future. Either way, stocks are financial assets with a value today that is based upon future cash flows. And just as with bonds, when inflation rises, the value of stocks today falls to reflect higher market rates.

We measure the value of stocks using the ratio of market price to current earnings (the price/earnings ratio, or P/E). When inflation rises, stock prices fall–so the ratio of P/E falls too. This enables new buyers of stocks to pay a lower price in order to receive a higher return to compensate for inflation. Conversely, falling inflation drives stock prices and P/E higher.

When the inflation rate falls into deflation, there’s another financial principle that causes P/E to fall. But we’ll save that for another day.

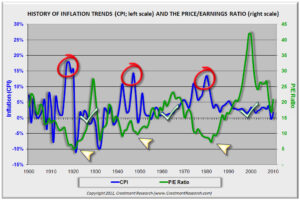
Note the graph below.  When blue line inflation is high (red circles), the green line P/E is below average (yellow arrows). Whenever inflation is low (green check marks), note that green line P/E is well above average.  (There’s one good incidence of deflation and lower P/E in the 1930s, but we’re saving that for another day…)  Inflation and P/E do bounce around a bit, yet the relationship follows the financial principles described above. Some people like the chart below (generally presented without the markings) and others prefer the one known as The Y Curve Effect. Both charts are available on the Crestmont Research website in the Stock Market section.

Probable Outcomes was written to stand alone, but depending upon your familiarity with the topics, Unexpected Returns can be a preferable start for someone who intends to read both.  If you only want one, then the question would be whether your interest is general and related to stock market returns and cycles, etc., or whether it more specifically concerns reasonable outlooks for the stock market over this decade.

Probable Outcomes is not a sequel or an update, but rather it is an application of the principles from Unexpected Returns to the current decade (with lots of extra and new details).  The second chapter of Probable Outcomes revisits many of the primary concepts from Unexpected Returns to refresh prior readers or to inform those who did not read it.  Some people who read Probable Outcomes first may choose to then read Unexpected Returns since it deals with some concepts that were not included in Probable Outcomes and will further enhance a reader’s understanding of those concepts.  Some recent readers of Unexpected Returns have found that Probable Outcomes helps to put the messages of Unexpected Returns into perspective by reflecting upon the period the first book was published–like reading an analyst’s report years after it was written from a historical perspective.  Neither book, however, provides a forecast; rather they provide the concepts and insights to enable readers to understand the dynamics that determine the investing environment and to understand which scenarios are reasonable. Further, both books offer encouragement that, with awareness, investors can plan and invest in ways that will enhance success.

According to Brian C.: “If I were to suggest that anyone read just one of your books I would have to say Probable Outcomes.  Unfortunately I can’t say why with specificity but the points came home more clearly as I read it.  That obviously could have been greatly enhanced from having read the first book.  It’s also more timely obviously as it relates to the future.  The first book gives a lot of credibility to your analysis since you were right about your predictions going forward to 2010 however the second book came more to life for me.”